【錯体化学】錯形成反応・生成定数と解離定数の解説 - 化学徒の備忘録(かがろく)|化学系ブログ

多くの金属イオンは、さまざまな配位子(錯形成剤)と平衡にある場合、ほとんど解離しない錯体を形成する。この錯形成を上手に利用し、ターゲットではない反応を遮蔽することで、錯体を分析化学に利用することができる。つまり、多くの金属イオン種は、錯滴定を利用することで正確に定量をすることができる。

多くの金属イオンは、配位数を満足させる非共有電子対をもつ多くの物質と溶液中で錯体を形成する。非共有電子対をもっている物質としては、例えばN、O、S原子などが挙げられる。金属イオンは電子対のアクセプターとなるルイス酸であり、錯形成剤は電子対のドナーとなるルイス塩基である。

配位子(リガンド)といわれる錯形成剤が、1つの金属イオンに対して何個配位するかは、金属イオンの配位数と配位子に存在している錯形成基の数によって決定される。

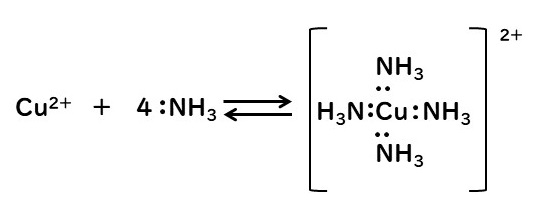
例えば、アンモニアは1つの非共有電子対をもつ錯形成剤であり、銅と錯形成する。

この場合には、銅はルイス酸であり、アンモニアはルイス塩基としてはたらいている。

ここでは、生成定数を考えるために、アンモニアと銀イオンを考える。この場合、2個のアンモニア分子は銀イオンと段階的に反応する。そのため生成定数(平衡定数) $K_f$ は次のように書くことができる。

$\mathrm{Ag^+ + NH_3 \rightleftharpoons Ag(NH_3)^+}$

$\displaystyle K_{f1} = \mathrm{ \frac{ [ Ag (NH_3)^+ ] }{ [ Ag^+ ] [ NH_3 ]} } = 2.5 \times 10^3$

$\mathrm{Ag(NH_3)^+ + NH_3 \rightleftharpoons Ag(NH_3)_2^+}$

$\displaystyle K_{f2} = \mathrm{ \frac{ [ Ag (NH_3)_2^+ ] }{ [ Ag(NH_3)^+ ] [ NH_3 ]} } = 1.0 \times 10^4$

ここで、 $K_{f1}、K_{f2}$ は逐次生成定数という。

全反応は各段階の総和である。全生成定数は生成定数の積によって求めることができる。

$\mathrm{Ag^+ + 2NH_3 \rightleftharpoons Ag(NH_3)_2^+}$

$\displaystyle K{f} = K_{f1} K_{f2} = \mathrm{ \frac{ [ Ag (NH_3)_2^+ ] }{ [ Ag^+ ] [ NH_3 ]^2} } = 2.5 \times 10^7$

単純な1:1の錯体の形成を、ここでは $\mathrm{M + L \rightleftharpoons ML }$ とする。この時、生成定数 $K_{f}$ は次のようになる。

$\displaystyle K_f = \mathrm{ \frac{ [ ML ] }{ [ M ] [ L ] }}$

生成定数は安定度定数( $K_S$ )ともいわれる。

平衡反応は解離反応として表される場合もある。その場合は、平衡定数を表す式の濃度の項は逆転することとなる。また、平衡定数は生成定数の逆数となり、解離定数( $K_d$ )といわれる。

例えば銀イオンとアンモニアの場合は解離定数は以下のようになる。

$\mathrm{ Ag(NH_3)_2^+ \rightleftharpoons Ag^+ + 2NH_3}$

$\displaystyle K_d = \frac{1}{K_f} = \mathrm{ \frac{ [ Ag^+ ] [ NH_3 ]^2}{ [ Ag (NH_3)_2^+ ] } } = 4.0 \times 10 ^{-8}$

生成定数と解離定数は、どちらを使っているかを正しく理解して扱っていれば、どちらを使っていても問題ない。