【錯体化学】配位子場理論と6配位正八面体型錯体・平面正方型錯体・ヤーンテラー効果

配位子場理論

配位子場理論は錯体の電子構造の理論として知られているものであるが、もともとはイオン結晶に関する理論である結晶場理論を錯体系に適用したものである。

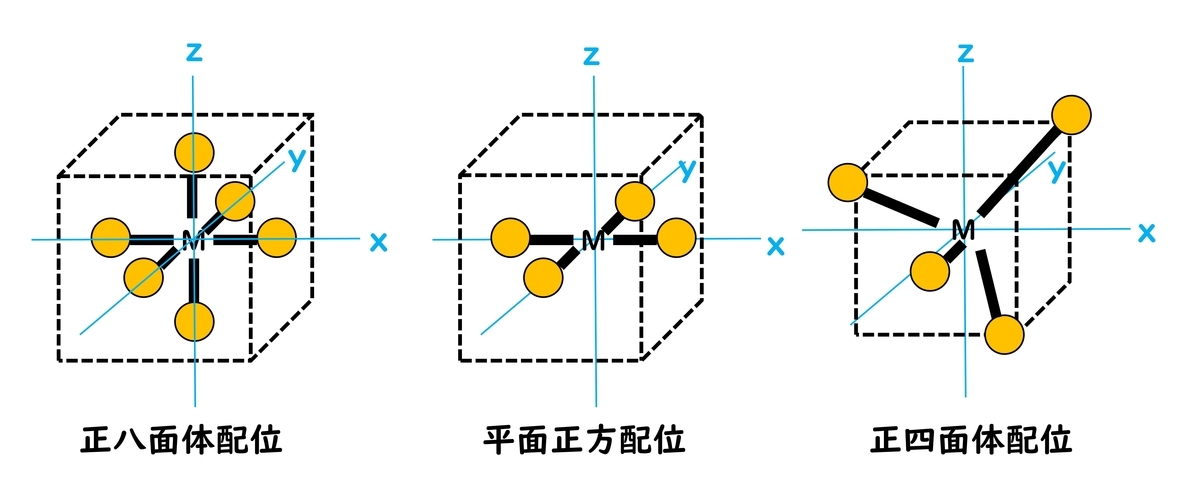
6配位正八面体型錯体

遷移金属の陽イオンの5つのd軌道は縮退している。そのため、5つのd軌道のエネルギーは等しいものとなっている。そこで、金属陽イオンの周りに球対称の負電場が来ると、静電相互作用によって全エネルギーは自由陽イオンのときよりも安定化する。しかし同時に、金属軌道の電子と負電場の反発相互作用によって不安定化もおこる。この安定化と不安定化によって、ある程度は相殺される。その変化を縦軸をエネルギーとして考えると、下図のようになる。

f:id:syerox:20220307105135j:plain — 錯体形成による電子エネルギー変化

球対称の負電場の代わりに6つの配位子が正八面体状に金属イオンに配位する場合について考える。配位子がおよぼす負電場を配位子場という。陰イオン性配位子の場合はその負電荷を考慮し、中性配位子の場合は双極子の負端(ローンペア)を考慮すると、金属陽イオンが置かれた位置を原点にとることで、直交座標系を設定することができる。

f:id:syerox:20220307110909j:plain — 直交座標系での配位子の位置

d_x²-_y²とd_z²軌道は座標軸方向にd_x、d_y、d_z軌道は座標軸の中間に向く。配位子を座標軸方向に置くと、d軌道と配位子の負電荷の反発相互作用によりe_g軌道 (d_x²-_y²とd_z²軌道)のほうがの不安定化が、t_2g軌道 (d_x、d_y、d_z軌道)の不安定化より大きく、全体としてそれだけ不安定化する。

配位子場の関与する軌道について考えるため、e_g軌道とt_2g軌道のエネルギー差が重要となるため、5つのd軌道全体のエネルギー重心をエネルギーの原点として考える。

e_g軌道が2つ、t_2g軌道が3つあるため、その間のエネルギー差 $\Delta _0$ とすると、e_g軌道が $+ \frac{3}{5}\Delta _0$ に、t_2g軌道が $- \frac{2}{5}\Delta _0$ に位置することになる。別の表記として $\Delta _0$ を10 Dqと表すと、e_g軌道が+6 Dq、t_2g軌道は-4 Dqに位置する。遷移金属イオンは0個から10個のd電子を有するため、これを分裂したd軌道に下から順番に詰めていくと、それぞれのイオンに対応する電子配置t_2g^xe_g^yが得られる。ここでxとyは電子数である。エネルギーの重心位置を0とするとこの電子配置に対するエネルギーはLFSE $= (0.4x+0.6y) \Delta_0$ となる。

上のLFSEで示した値を配位子場安定化エネルギーという。負の値が大きいほどその電子配置は安定となる。配位子場安定化エネルギーはdブロック遷移金属錯体の性質を説明するうえでも重要となる。

電子がt_2g軌道とe_g軌道に分裂した軌道に入る場合、軌道のエネルギーバンド以外にも、もう一つ考慮することがある。

一つの軌道には2個の電子がスピン逆平行に入ることができる。しかし、同じ軌道に2個の電子が入ると強い静電相互反発作用が生じる。この相互作用を電子対形成エネルギー $P$ という。d電子数が3個以下であれば、t_2g軌道に平行スピンで入ることによって、もっともエネルギーが低くなる。つまり電子配置はt_2g¹,t_2g²,t_2g³となる。

しかし4つ目の電子が入る場合には考える必要があることがある。軌道のエネルギーからは低いほうのt_2g軌道に電子を入れたほうが得である。しかし、同じ軌道に2つの電子を入れると $P$ のエネルギーが余分に必要である。つまり、全安定化エネルギーは以下のようになる。

$- 0.4 \delta _0 \times 4 + P = -1.6 \Delta_0 + P$

もし4つ目の電子を上のe_g軌道に入れる場合、それだけエネルギー的には損であるが、すべて平行スピンになるため、 $P$ が不要となる。

つまり全安定化エネルギーは次のようになる。

$- 0.4 \delta _0 \times 3 +0.6 \Delta_0 = -0.6 \Delta_0$

どちらの電子配置がエネルギー的に有利であるかは、 $-1.6 \Delta_0 + P$ と $-0.6 \Delta_0$ の大小関係で決まることになる。 $\Delta_0 \gt P$ である場合はt_2g⁴が有利となる。このt_2g⁴が有利な場合を低スピン電子配置という。 $\Delta_0 \lt P$ である場合はt_2g³e_g¹が有利となる。このt_2g³e_g¹が有利な場の場合を高スピン電子配置という。

d⁵、d⁶、d⁷のときにも同様に低スピンと高スピンの電子配置の場合がある。低スピン配置の場合はt_2g⁵、t_2g⁶、t_2g⁷をとる。高スピン配置の場合はt_2g³e_g²、t_2g⁴e_g²、t_2g⁵e_g²をとる。

配位子場分裂パラメーター $\Delta_0$ は配位子の種類と金属によって決まる。一方で、電子対形成エネルギー $P$ はほぼ一定である。しかしながら、金属に依存する値となる。

平面正方型錯体

4つの配位子が金属を含む平面に位置する錯体を平面正方型錯体という。この平面正方型錯体におけるd軌道のエネルギーレベルを考える場合は、6配位正八面体型錯体のエネルギーレベルを出発点として考えると、考えやすくなる。

直交座標方向にある配位子のうちz軸の方向の2つの配位子を中心金属から遠ざけていき、最終的に4つの配位子のみをx、y平面内に残すという過程を考える。この場合、配位子とd_z²とd_xzとd_yz軌道の電子の反発相互作用が次第に小さくなる。そのため、これらの軌道のエネルギーレベルは低下する。一方で、2個の配位子が失われると残りの4個の配位子が金属に接近するため、d_x²-_y²とd_xy軌道のエネルギーレベルは上昇する。その結果、エネルギーレベルの大小は d_xzとd_yz< d_xy << d_x²-_y² の順番になる

d⁸構造をもつRh⁺、Ir⁺、Pd²⁺、Pt²⁺、Au³⁺の錯体が正方平面型になりやすい理由はd_x²-_y²軌道が空になり下の4つの軌道を8つの電子が占有する電子構造が安定であるからである。

四面体型錯体

[CoX₄]^2-(X = Cl, B, I, Ni(CO)₄)などの4配位錯体の中で、配位子の空間配置が金属を中心として正四面体頂点にあり、配位多面体が四面体となるものが四面体型錯体である。

正八面体型錯体の場合と同様に直交座標系の原点に金属をおいた場合、e軌道(d_x²-_y²とd_z²)は配位子方向にないが、t₂軌道(d_xy、d_yz、d_xz）は配位子方向に近い。よって電子間反発相互作用はt₂の組のほうが大きいため不安定化し、相対的に3の組が安定化する。

つまり、4つの配位子がおよぼす配位子場も、中心金属の5重縮退軌道を二重縮退のeと三重縮退のt₂の2組に分裂させる。エネルギー分裂を $\Delta _t$ とするとt₂は $+\frac{2}{5} \Delta _t$ 、eは $-\frac{3}{5} \Delta _t$ のエネルギーをもつ。

配位子の数が6配位正八面体型錯体と比べて、4/6 = 2/3であることと配位子位置とd軌道の重なりが小さいために、正四面体型錯体における配位子場分裂 $\delta _t$ は正八面体型錯体における $\Delta _0$ の約半分以下になることが知られている。

よって正四面体型錯体では、高スピン型の電子配置のみが知られている。

ヤーンテラー効果

対称性の高い非直線状他原子分子の軌道が縮退している場合、分子がゆがむことによって対称性が低くなると縮退が解け、低いエネルギー状態となる。これをヤーンテラー効果という。よく知られているものとして、6配位2価銅錯体における配位構造の正八面体から上下方向への歪みが生じるものがある。

2価の銅イオンはd⁹であるため、正八面体構造におけるe_g軌道には3つの電子がある。もしe_g軌道が分裂して、下の軌道に2つ、上の軌道に1つの電子が入ると、これら2つの軌道間のエネルギー差 $\delta$ の1/2だけエネルギー的に得になる。つまりz軸方向に正方歪みを起こすと、エネルギー的に有利になる。