【量子化学】二粒子系の波動方程式の扱い方の解説 - 化学徒の備忘録(かがろく)|化学系ブログ

二粒子系の波動方程式

二粒子系の波動方程式は次のように考えることで、粒子1個の問題として取り扱うことができるようになり、簡単になる。

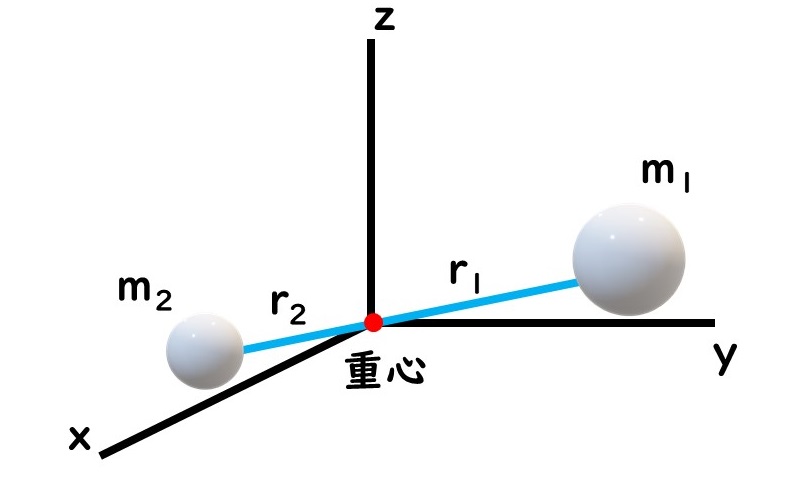
質量が $m_1$ と $m_2$ の2個の粒子が、それぞれ速度 $v_1$ と $v_2$ をもっている。そして、位置エネルギー $U$ で運動しているとする。

この時のエネルギー $E$ は次の式で求めることができる。

$\displaystyle E = \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 + U$

各粒子( $i=1, 2$ )の座標を( $x_i, y_i , z_i$ )とする。このとき重心の座標( $X, Y, Z$ )は次の式のように表すことができる。

$\displaystyle X = \frac{m_1 x_1 + m_2 x_2}{m_1 + m_2}$

$\displaystyle Y = \frac{m_1 y_1 + m_2 y_2}{m_1 + m_2}$

$\displaystyle Z = \frac{m_1 z_1 + m_2 z_2}{m_1 + m_2}$

各粒子の速度を表すベクトル[texV_i]は、各座標成分の時間微分となる。つまり次の式のようになる。

$\displaystyle V_i = \left ( \frac{dx_i}{dt} , \frac{dy_i}{dt} , \frac{dz_i}{dt} \right ) (i=1, 2)$

重心の速度を $V_G$ とする。重心の速度は各座標成分を時間で微分して求めることができるため、次のように表すことができる。

$\displaystyle V_G = \frac{m_1 V_1 + m_2 V_2}{m_1 + m_2}$

ここで、粒子に着目して座標を考える。1つ目の粒子の座標を基準にして、2つ目の粒子の座標を考えると、相対座標( $x, y, z$ )を次のように表すことができる。

$x =x_2 - x_1$

$y =y_2 - y_1$

$z =z_2 - z_1$

相対速度 $V$ は、相対座標の時間変化であるため、2つの粒子を考えることで、次のように表すことができる。

$V =V_2 - V_1$

重心の運動は粒子間の相対運動とは独立している。そして、粒子同士の相対的な位置を保ったまま、粒子が並んで運動することから、並進運動という。

二粒子系のエネルギーを相対運動と並進運動の速度を用いて表すと次のようになる。

$\displaystyle E=\frac{1}{2} (m_1 + m_2) V_G^2 + \frac{1}{2} \mu V^2 + U$

上の式の最初の項は並進運動(重心運動)の運動エネルギーを表す。第2項は相対運動の運動エネルギーを表す。第2項の $\mu$ は2個の各粒子の質量の逆数の和の逆数であり換算質量といわれる。換算質量は次のように表すことができる。

$\displaystyle \mu = \frac{1}{ \frac{1}{m_1} + \frac{1}{m_2} }$

質量 $m_1$ と $m_2$ の2個の球が距離 $r = r_1 + r_2$ で結合している。

この時、重心を座標の原点に固定することによって、二粒子系のエネルギーの第1項が0となって消えるため、第2項の $\frac{1}{2} \mu V^2$ のみが運動エネルギーとして残る。そのため、2個の相対運動は換算質量 $\mu$ をもつ1個の粒子の運動として取り扱うことができる。

その結果、以下のように1粒子の波動方程式と同じ形で表すことができる。

$\displaystyle \left ( - \frac{\hbar}{2 \mu} \Delta + U \right ) \psi = E \psi$

こういった場合、原点からの距離 $r$ が重要となる。そのため、直行座標( $x, y, z$ )の代わりに三次元の極座標( $r, \theta , \varphi$ ) を変数にとる。

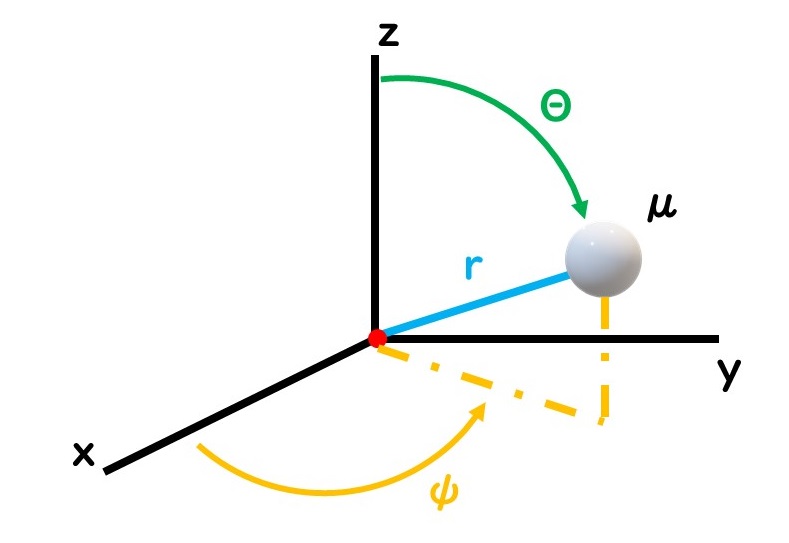
この極座標は、原点からの距離 $r ( 0 \le r \lt \infty )$ 、 $z$ 軸からのずれの角度 $\theta ( 0 \le \theta \le \pi )$ 、 $x-y$ 面に投影した点が $x$ 軸からどれだけずれているかを表す角度 $\varphi ( 0 \le \varphi \lt 2 \pi )$ を用いている。

極座標を用いた場合、体積要素 $\mathrm{d} \tau = \mathrm{d} x \mathrm{d} y \mathrm{d} z$ は次のように表すことができる。

$\tau = \mathrm{d} x \mathrm{d} y \mathrm{d} z = r^2 \sin \theta \mathrm{d} r \mathrm{d} \theta \mathrm{d} \varphi$

ラプラシアン $\Delta$ は次のように表すことができる。

$\displaystyle \Delta = \frac{1}{r^2} \frac{ \partial }{ \partial r} \left ( r^2 \frac{ \partial }{ \partial r} \right ) + \frac{1}{r^2} \Lambda$

ここで $\Lambda$ はルジャンドリアンといわれ、二つの角度 $\theta$ と $\varphi$ に依存する演算子であり、次の式のように求めることができる。

$\displaystyle \Lambda = \frac{1}{\sin \theta} \frac{ \partial}{ \partial \theta } \sin \theta \frac{ \partial}{ \partial \theta } + \frac{1}{\sin ^2 \theta } \frac{ \partial ^2}{ \partial \varphi ^2}$

ラプラシアンやルジャンドリアンの式の右辺の演算子は、演算を行う関数に対して、各項の右端部分から順番に演算を行う。