化学徒の備忘録(かがろく)|化学系ブログ

理系の筆者が化学系の用語や論文、動画、ノウハウなどを紹介する化学ブログ

【物理化学】部分モル体積の求め方の図的方法

物理化学用語解説

部分モル体積の求め方

部分モル体積の求め方として、図的方法といわれるものがある。

ここでは、2成分系の場合について考える。この時、平均モル体積 $\bar{V}$ は以下の式で求めることができる。

$\displaystyle \bar{V} = \frac{V}{ n_A + n_B }= x_A v_A + x_B v_B = \frac{x_A M_A + x_B M_B}{\rho}$

$V$ は全体積である。 $n_A$ と $n_B$ は成分AおよびBの物質量 (mol)である。 $M_A$ と $M_B$ は成分AおよびBのモル質量である。 $x_A$ と $x_B$ は成分AおよびBのモル分率である。

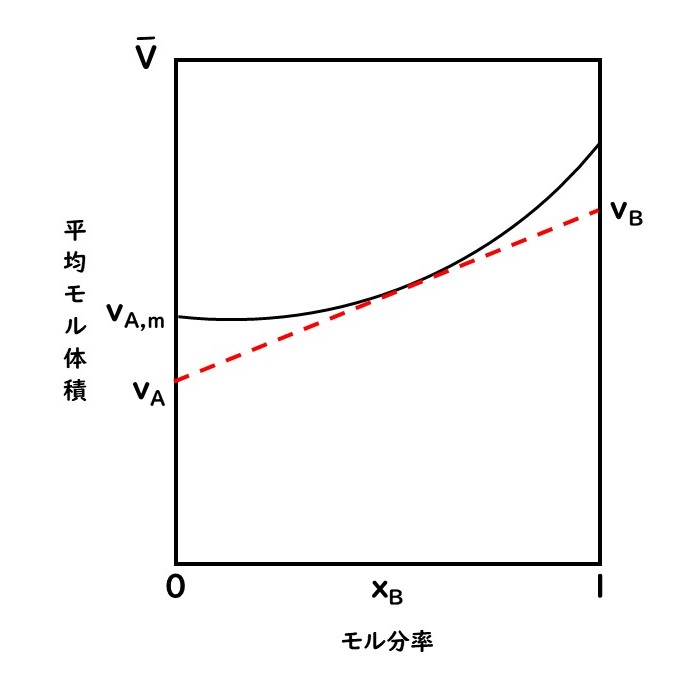
そこで、溶液の密度 $\rho$ の測定から決定して、モル分率 $x_B$ に対して図を書くと下のようになる。この曲線に対して、任意のモル分率に引いた接線が $x_B =0$ と $x_B =1$ での縦軸と交わる切片から、それぞれの成分AとBの部分モル体積 $v_A$ と $v_B$ が決定できる。

ここで下の関係が成り立つ。

$V = n_A v_A + n_B v_B$

このことから、次の関係が成り立つ。

$\mathrm{d} V = v_A \mathrm{d} n_A + v_B \mathrm{d} n_B + n_A \mathrm{d} v_A+ n_B \mathrm{d} v_B$

この上の式を下の式と比較する。

$\mathrm{d} V = v_A \mathrm{d} n_A + v_B \mathrm{d} n_B$

その結果、下の関係を導くことができる。

$n_A \mathrm{d} v_A+ n_B \mathrm{d} v_B = 0$

この式の両辺を全物質量 $n = n_A + n_B$ で割ると次のようになる。

$x_A \mathrm{d} v_A+ x_B \mathrm{d} v_B = 0$

また以下の関係が成り立つ。

$x_A + x_B = 1$

$\mathrm{d} x_A = -\mathrm{d} x_B$

よって、上の式を用いると、温度と圧力が一定の場合の平均モル体積の全微分は以下の通りになる。

$\mathrm{d} \bar{V} = v_A \mathrm{d} x_A + v_B \mathrm{d} x_B = ( v_B- v_A ) \mathrm{d} x_B$

この関係から、 $\bar{V}-x_B$ の曲線にモル分率 $x_B$ で引いた接線の傾きが以下の式で与えられる。

$\displaystyle \left( \frac{ \partial \bar{V}}{\partial x_B} \right)_{T,p} = v_B -v_A$

よって $\bar{V}-x_B$ の曲線にモル分率 $x_B$ で引いた接線の式が導ける。

$\bar{V} = (v_B -v_A) x_B + v_A$